Let
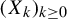 $(X_k)_{k\geq 0}$
be a stationary and ergodic process with joint distribution
$(X_k)_{k\geq 0}$
be a stationary and ergodic process with joint distribution
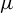 $\mu $
, where the random variables
$\mu $
, where the random variables
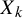 $X_k$
take values in a finite set
$X_k$
take values in a finite set
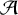 $\mathcal {A}$
. Let
$\mathcal {A}$
. Let
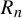 $R_n$
be the first time this process repeats its first n symbols of output. It is well known that
$R_n$
be the first time this process repeats its first n symbols of output. It is well known that
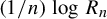 $({1}/{n})\log R_n$
converges almost surely to the entropy of the process. Refined properties of
$({1}/{n})\log R_n$
converges almost surely to the entropy of the process. Refined properties of
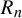 $R_n$
(large deviations, multifractality, etc) are encoded in the return-time
$R_n$
(large deviations, multifractality, etc) are encoded in the return-time
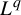 $L^q$
-spectrum defined as
$L^q$
-spectrum defined as
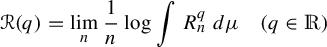
provided the limit exists. We consider the case where
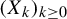 $(X_k)_{k\geq 0}$
is distributed according to the equilibrium state of a potential
$(X_k)_{k\geq 0}$
is distributed according to the equilibrium state of a potential
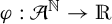 with summable variation, and we prove that
with summable variation, and we prove that
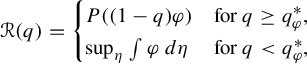
where
 $P((1-q)\varphi )$
is the topological pressure of
$P((1-q)\varphi )$
is the topological pressure of
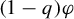 $(1-q)\varphi $
, the supremum is taken over all shift-invariant measures, and
$(1-q)\varphi $
, the supremum is taken over all shift-invariant measures, and
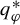 $q_\varphi ^*$
is the unique solution of
$q_\varphi ^*$
is the unique solution of
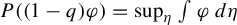 $P((1-q)\varphi ) =\sup _\eta \int \varphi \,d\eta $
. Unexpectedly, this spectrum does not coincide with the
$P((1-q)\varphi ) =\sup _\eta \int \varphi \,d\eta $
. Unexpectedly, this spectrum does not coincide with the
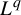 $L^q$
-spectrum of
$L^q$
-spectrum of
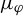 $\mu _\varphi $
, which is
$\mu _\varphi $
, which is
 $P((1-q)\varphi )$
, and it does not coincide with the waiting-time
$P((1-q)\varphi )$
, and it does not coincide with the waiting-time
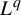 $L^q$
-spectrum in general. In fact, the return-time
$L^q$
-spectrum in general. In fact, the return-time
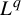 $L^q$
-spectrum coincides with the waiting-time
$L^q$
-spectrum coincides with the waiting-time
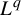 $L^q$
-spectrum if and only if the equilibrium state of
$L^q$
-spectrum if and only if the equilibrium state of
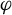 $\varphi $
is the measure of maximal entropy. As a by-product, we also improve the large deviation asymptotics of
$\varphi $
is the measure of maximal entropy. As a by-product, we also improve the large deviation asymptotics of
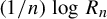 $({1}/{n})\log R_n$
.
$({1}/{n})\log R_n$
.
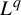 $L^q$
-spectrum for equilibrium states with potentials of summable variation
$L^q$
-spectrum for equilibrium states with potentials of summable variation