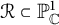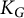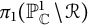4 results
On irreducible representations of Fuchsian groups
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 27 August 2024, pp. 970-990
- Print publication:
- December 2024
-
- Article
-
- You have access
- HTML
- Export citation
Computing a categorical Gromov–Witten invariant
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 7 / July 2020
- Published online by Cambridge University Press:
- 18 June 2020, pp. 1275-1309
- Print publication:
- July 2020
-
- Article
- Export citation
Gromov–Witten theory and Donaldson–Thomas theory, II
-
- Journal:
- Compositio Mathematica / Volume 142 / Issue 5 / September 2006
- Published online by Cambridge University Press:
- 25 September 2006, pp. 1286-1304
- Print publication:
- September 2006
-
- Article
-
- You have access
- Export citation
Gromov–Witten theory and Donaldson–Thomas theory, I
-
- Journal:
- Compositio Mathematica / Volume 142 / Issue 5 / September 2006
- Published online by Cambridge University Press:
- 25 September 2006, pp. 1263-1285
- Print publication:
- September 2006
-
- Article
-
- You have access
- Export citation