1 results
On supercritical nonlinear Schrödinger equations with ellipse-shaped potentials
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 6 / December 2020
- Published online by Cambridge University Press:
- 02 December 2019, pp. 3187-3215
- Print publication:
- December 2020
-
- Article
- Export citation
-
In this paper, we study the existence and concentration of normalized solutions to the supercritical nonlinear Schrödinger equation
where μq is the Lagrange multiplier. For ellipse-shaped potentials V(x), we show that for q > 2 close to 2, the equation admits an excited solution uq, and furthermore, we study the limiting behaviour of uq when q → 2+. Particularly, we describe precisely the blow-up formation of the excited state uq.
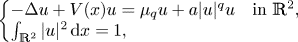\[ \left\{\begin{array}{@{}ll} -\Delta u + V(x) u = \mu_q u + a \vert u \vert ^q u & {\rm in}\ \mathbb{R}^2,\\ \int_{\mathbb{R}^2} \vert u \vert ^2\,{\rm d}x =1, & \end{array} \right.\]
