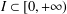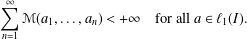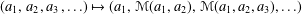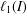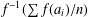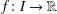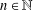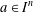1 results
WEAKENING OF THE HARDY PROPERTY FOR MEANS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 09 July 2019, pp. 118-129
- Print publication:
- February 2020
-
- Article
- Export citation
-
The aim of this paper is to find a broad family of means defined on a subinterval of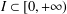
$I\subset [0,+\infty )$ such that Equivalently, the averaging operator
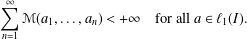$$\begin{eqnarray}\mathop{\sum }_{n=1}^{\infty }\mathscr{M}(a_{1},\ldots ,a_{n})<+\infty \quad \text{for all }a\in \ell _{1}(I).\end{eqnarray}$$
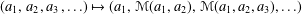$(a_{1},\,a_{2},a_{3}\,,\ldots )\mapsto (a_{1},\,\mathscr{M}(a_{1},a_{2}),\,\mathscr{M}(a_{1},a_{2},a_{3}),\ldots )$ is a selfmapping of 
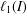$\ell _{1}(I)$. This property is closely related to the so-called Hardy inequality for means (which additionally requires boundedness of this operator). We prove that these two properties are equivalent in a broad family of so-called Gini means. Moreover, we show that this is not the case for quasi-arithmetic means, that is functions 
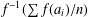$f^{-1}(\sum f(a_{i})/n)$, where 
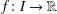$f:I\rightarrow \mathbb{R}$ is continuous and strictly monotone, 
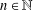$n\in \mathbb{N}$ and 
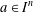$a\in I^{n}$. However, the weak Hardy property is localisable for this family.
