Let 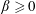 $\unicode[STIX]{x1D6FD}\geqslant 0$, let
$\unicode[STIX]{x1D6FD}\geqslant 0$, let 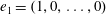 $e_{1}=(1,0,\ldots ,0)$ be a unit vector on
$e_{1}=(1,0,\ldots ,0)$ be a unit vector on 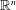 $\mathbb{R}^{n}$, and let
$\mathbb{R}^{n}$, and let 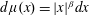 $d\unicode[STIX]{x1D707}(x)=|x|^{\unicode[STIX]{x1D6FD}}dx$ be a power weighted measure on
$d\unicode[STIX]{x1D707}(x)=|x|^{\unicode[STIX]{x1D6FD}}dx$ be a power weighted measure on 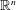 $\mathbb{R}^{n}$. For
$\mathbb{R}^{n}$. For 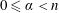 $0\leqslant \unicode[STIX]{x1D6FC}<n$, let
$0\leqslant \unicode[STIX]{x1D6FC}<n$, let 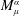 $M_{\unicode[STIX]{x1D707}}^{\unicode[STIX]{x1D6FC}}$ be the centered Hardy-Littlewood maximal function and fractional maximal functions associated with measure
$M_{\unicode[STIX]{x1D707}}^{\unicode[STIX]{x1D6FC}}$ be the centered Hardy-Littlewood maximal function and fractional maximal functions associated with measure 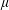 $\unicode[STIX]{x1D707}$. This paper shows that for
$\unicode[STIX]{x1D707}$. This paper shows that for 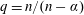 $q=n/(n-\unicode[STIX]{x1D6FC})$,
$q=n/(n-\unicode[STIX]{x1D6FC})$, 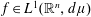 $f\in L^{1}(\mathbb{R}^{n},d\unicode[STIX]{x1D707})$,
$f\in L^{1}(\mathbb{R}^{n},d\unicode[STIX]{x1D707})$, 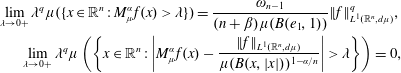 $$\begin{eqnarray}\displaystyle \lim _{\unicode[STIX]{x1D706}\rightarrow 0+}\unicode[STIX]{x1D706}^{q}\unicode[STIX]{x1D707}(\{x\in \mathbb{R}^{n}:M_{\unicode[STIX]{x1D707}}^{\unicode[STIX]{x1D6FC}}f(x)>\unicode[STIX]{x1D706}\})=\frac{\unicode[STIX]{x1D714}_{n-1}}{(n+\unicode[STIX]{x1D6FD})\unicode[STIX]{x1D707}(B(e_{1},1))}\Vert f\Vert _{L^{1}(\mathbb{R}^{n},d\unicode[STIX]{x1D707})}^{q}, & & \displaystyle \nonumber\\ \displaystyle \lim _{\unicode[STIX]{x1D706}\rightarrow 0+}\unicode[STIX]{x1D706}^{q}\unicode[STIX]{x1D707}\left(\left\{x\in \mathbb{R}^{n}:\left|M_{\unicode[STIX]{x1D707}}^{\unicode[STIX]{x1D6FC}}f(x)-\frac{\Vert f\Vert _{L^{1}(\mathbb{R}^{n},d\unicode[STIX]{x1D707})}}{\unicode[STIX]{x1D707}(B(x,|x|))^{1-\unicode[STIX]{x1D6FC}/n}}\right|>\unicode[STIX]{x1D706}\right\}\right)=0, & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \lim _{\unicode[STIX]{x1D706}\rightarrow 0+}\unicode[STIX]{x1D706}^{q}\unicode[STIX]{x1D707}(\{x\in \mathbb{R}^{n}:M_{\unicode[STIX]{x1D707}}^{\unicode[STIX]{x1D6FC}}f(x)>\unicode[STIX]{x1D706}\})=\frac{\unicode[STIX]{x1D714}_{n-1}}{(n+\unicode[STIX]{x1D6FD})\unicode[STIX]{x1D707}(B(e_{1},1))}\Vert f\Vert _{L^{1}(\mathbb{R}^{n},d\unicode[STIX]{x1D707})}^{q}, & & \displaystyle \nonumber\\ \displaystyle \lim _{\unicode[STIX]{x1D706}\rightarrow 0+}\unicode[STIX]{x1D706}^{q}\unicode[STIX]{x1D707}\left(\left\{x\in \mathbb{R}^{n}:\left|M_{\unicode[STIX]{x1D707}}^{\unicode[STIX]{x1D6FC}}f(x)-\frac{\Vert f\Vert _{L^{1}(\mathbb{R}^{n},d\unicode[STIX]{x1D707})}}{\unicode[STIX]{x1D707}(B(x,|x|))^{1-\unicode[STIX]{x1D6FC}/n}}\right|>\unicode[STIX]{x1D706}\right\}\right)=0, & & \displaystyle \nonumber\end{eqnarray}$$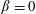 $\unicode[STIX]{x1D6FD}=0$. Meanwhile, the corresponding results for the un-centered maximal functions as well as the fractional integral operators with respect to measure
$\unicode[STIX]{x1D6FD}=0$. Meanwhile, the corresponding results for the un-centered maximal functions as well as the fractional integral operators with respect to measure 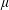 $\unicode[STIX]{x1D707}$ are also obtained.
$\unicode[STIX]{x1D707}$ are also obtained.

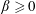
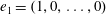
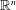
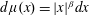
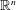
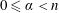
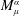
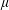
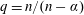
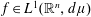
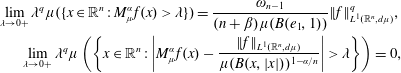
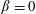
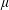
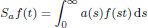
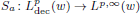 was completely solved, the characterization of the weights
was completely solved, the characterization of the weights 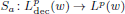 is bounded is still open for the case in which
is bounded is still open for the case in which 