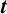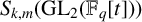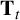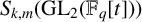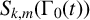An exact control theorem is proven for nearly ordinary $p$-adic automorphic forms on symplectic and unitary groups over
totally real fields if the algebraic group is split at $p$. In particular, a given nearly ordinary holomorphic Hecke
eigenform can be lifted to a family of holomorphic Hecke eigenforms indexed by weights of the standard maximal split
torus of the group. Their $q$-expansion coefficients are Iwasawa functions on the Iwasawa algebra of ${\mathbb{Z}}_p$-points of
the split torus. The method is applicable to any reductive algebraic groups yielding Shimura varieties of PEL type
under mild assumptions on the existence of integral toroidal compactification of the variety. Even in the Hilbert
modular case, the result contains something new: freeness of the universal nearly ordinary Hecke algebra over the
Iwasawa algebra, which eluded my scrutiny when I studied general theory of the $p$-adic Hecke algebra in the 1980s.
AMS 2000 Mathematics subject classification: Primary 11F03; 11F30; 11F33; 11F41; 11F60; 11G15; 11G18
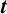 $\boldsymbol {t}$
$\boldsymbol {t}$