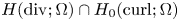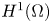We derive a global higher regularity result for weak solutions of the linear relaxed micromorphic model on smooth domains. The governing equations consist of a linear elliptic system of partial differential equations that is coupled with a system of Maxwell-type. The result is obtained by combining a Helmholtz decomposition argument with regularity results for linear elliptic systems and the classical embedding of $H(\operatorname {div};\Omega )\cap H_0(\operatorname {curl};\Omega )$ into $H^1(\Omega )$.

We consider H(curl;Ω)-elliptic problems that have been discretized bymeans of Nédélec's edge elements on tetrahedral meshes. Suchproblems occur in the numerical computation of eddy currents. From the defectequation we derive localized expressions that can be used as a posteriori error estimators to control adaptiverefinement. Under certain assumptions on material parameters and computational domains, we derive local lower bounds and a global upper bound for the total error measured in the energy norm. The fundamental tool in the numerical analysis is a Helmholtz-type decomposition of the error into an irrotational part and a weakly solenoidal part.