3 results
A WEIGHTED
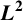 $\boldsymbol {L}^{\boldsymbol {2}}$ ESTIMATE OF COMMUTATORS OF BOCHNER–RIESZ OPERATORS FOR HERMITE OPERATOR
$\boldsymbol {L}^{\boldsymbol {2}}$ ESTIMATE OF COMMUTATORS OF BOCHNER–RIESZ OPERATORS FOR HERMITE OPERATOR
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 116 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 15 January 2024, pp. 308-330
- Print publication:
- June 2024
-
- Article
-
- You have access
- HTML
- Export citation
Spectral Theory of the Hermite Operator on Lp(Rn)
-
- Journal:
- Mathematical Modelling of Natural Phenomena / Volume 9 / Issue 5 / 2014
- Published online by Cambridge University Press:
- 17 July 2014, pp. 39-43
- Print publication:
- 2014
-
- Article
- Export citation
The ρ-variation of the heat semigroup in the Hermitian setting: behaviour in L∞
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 54 / Issue 3 / October 2011
- Published online by Cambridge University Press:
- 14 June 2011, pp. 569-585
-
- Article
-
- You have access
- Export citation

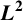
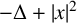
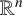
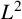
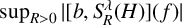
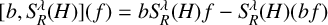
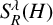
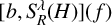
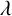

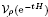 , ρ > 2, be the ρ-variation of the heat semigroup associated to the harmonic oscillator
, ρ > 2, be the ρ-variation of the heat semigroup associated to the harmonic oscillator 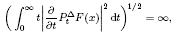
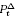 is the classical Poisson kernal in ℝ.
is the classical Poisson kernal in ℝ.