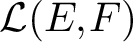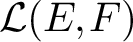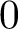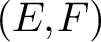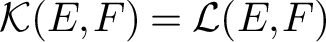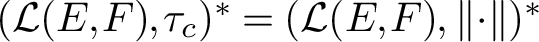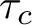In this article, we provide necessary and sufficient conditions for the existence of non-norm-attaining operators in
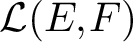 $\mathcal {L}(E, F)$
. By using a theorem due to Pfitzner on James boundaries, we show that if there exists a relatively compact set K of
$\mathcal {L}(E, F)$
. By using a theorem due to Pfitzner on James boundaries, we show that if there exists a relatively compact set K of
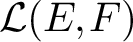 $\mathcal {L}(E, F)$
(in the weak operator topology) such that
$\mathcal {L}(E, F)$
(in the weak operator topology) such that
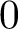 $0$
is an element of its closure (in the weak operator topology) but it is not in its norm-closed convex hull, then we can guarantee the existence of an operator that does not attain its norm. This allows us to provide the following generalisation of results due to Holub and Mujica. If E is a reflexive space, F is an arbitrary Banach space and the pair
$0$
is an element of its closure (in the weak operator topology) but it is not in its norm-closed convex hull, then we can guarantee the existence of an operator that does not attain its norm. This allows us to provide the following generalisation of results due to Holub and Mujica. If E is a reflexive space, F is an arbitrary Banach space and the pair
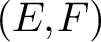 $(E, F)$
has the (pointwise-)bounded compact approximation property, then the following are equivalent:
$(E, F)$
has the (pointwise-)bounded compact approximation property, then the following are equivalent:
-
(i)
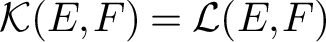 $\mathcal {K}(E, F) = \mathcal {L}(E, F)$
;
$\mathcal {K}(E, F) = \mathcal {L}(E, F)$
;
-
(ii) Every operator from E into F attains its norm;
-
(iii)
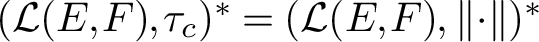 $(\mathcal {L}(E,F), \tau _c)^* = (\mathcal {L}(E, F), \left \Vert \cdot \right \Vert )^*$
,
$(\mathcal {L}(E,F), \tau _c)^* = (\mathcal {L}(E, F), \left \Vert \cdot \right \Vert )^*$
,
where
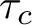 $\tau _c$
denotes the topology of compact convergence. We conclude the article by presenting a characterisation of the Schur property in terms of norm-attaining operators.
$\tau _c$
denotes the topology of compact convergence. We conclude the article by presenting a characterisation of the Schur property in terms of norm-attaining operators.