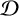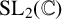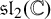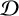In this paper we prove an analogue of Jantzen's sum formula for the $q$-Weyl modules of the $q$-Schur algebra and, as a consequence, derive the analogue of Schaper's theorem for the $q$-Specht modules of the Hecke algebras of type $\bf A$. We apply these results to classify the irreducible $q$-Weyl modules and the irreducible ($e$-regular) $q$-Specht modules, defined over any field. In turn, this allows us to identify all of the ordinary irreducible representations of the finite general linear group $GL_n(q)$ which remain irreducible modulo a prime $p$ not dividing~$q$.
1991 Mathematics Subject Classification: 20C32.