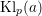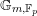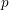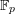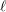9 results
Random walks and the “Euclidean” association scheme in finite vector spaces
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 24 May 2024, pp. 1-22
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Primitive rational points on expanding horocycles in products of the modular surface with the torus
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 6 / June 2021
- Published online by Cambridge University Press:
- 04 June 2020, pp. 1706-1750
- Print publication:
- June 2021
-
- Article
- Export citation
Kloosterman paths and the shape of exponential sums
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 7 / July 2016
- Published online by Cambridge University Press:
- 15 April 2016, pp. 1489-1516
- Print publication:
- July 2016
-
- Article
- Export citation
Galois representations attached to moments of Kloosterman sums and conjectures of Evans
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 1 / January 2015
- Published online by Cambridge University Press:
- 07 October 2014, pp. 68-120
- Print publication:
- January 2015
-
- Article
- Export citation
POWER-FREE VALUES OF THE POLYNOMIAL t1⋯tr−1
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 85 / Issue 1 / February 2012
- Published online by Cambridge University Press:
- 23 September 2011, pp. 154-163
- Print publication:
- February 2012
-
- Article
-
- You have access
- Export citation
NONVANISHING OF JACOBI POINCARÉ SERIES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 89 / Issue 2 / October 2010
- Published online by Cambridge University Press:
- 12 January 2011, pp. 165-179
- Print publication:
- October 2010
-
- Article
-
- You have access
- Export citation
The orthogonality of Hecke eigenvalues
-
- Journal:
- Compositio Mathematica / Volume 143 / Issue 3 / May 2007
- Published online by Cambridge University Press:
- 04 December 2007, pp. 541-565
- Print publication:
- May 2007
-
- Article
-
- You have access
- Export citation
On the pseudorandomness of the signs of Kloosterman sums
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 77 / Issue 3 / December 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 425-436
- Print publication:
- December 2004
-
- Article
-
- You have access
- Export citation
On Kloosterman Sums with Oscillating Coefficients
-
- Journal:
- Canadian Mathematical Bulletin / Volume 42 / Issue 3 / 01 September 1999
- Published online by Cambridge University Press:
- 20 November 2018, pp. 285-290
- Print publication:
- 01 September 1999
-
- Article
-
- You have access
- Export citation