Entropy functionals of probability densities feature importantly in classifying certain finite-state stationary stochastic processes, in discriminating among competing hypotheses, in characterizing Gaussian, Poisson, and other densities, in describing information processes, and in other contexts. Two general types of problems are considered. For a given parametric family of densities 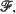 the member of maximal (or sometimes minimal) entropy is ascertained. Secondly, we determine a natural (partial) ordering over
the member of maximal (or sometimes minimal) entropy is ascertained. Secondly, we determine a natural (partial) ordering over 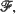 for which the entropy functional is monotone. The examples include the multiparameter binomial, multiparameter negative binomial, some classes of log concave densities, and others.
for which the entropy functional is monotone. The examples include the multiparameter binomial, multiparameter negative binomial, some classes of log concave densities, and others.