1 results
Stability of extremes with random sample size
-
- Journal:
- Journal of Applied Probability / Volume 26 / Issue 4 / December 1989
- Published online by Cambridge University Press:
- 14 July 2016, pp. 734-743
- Print publication:
- December 1989
-
- Article
- Export citation
-
A non-degenerate distribution function F is called maximum stable with random sample size if there exist positive integer random variables Nn, n = 1, 2, ···, with P(Nn = 1) less than 1 and tending to 1 as n → ∞ and such that F and the distribution function of the maximum value of Nn independent observations from F (and independent of Nn) are of the same type for every index n. By proving the converse of an earlier result of the author, it is shown that the set of all maximum stable distribution functions with random sample size consists of all distribution functions F satisfying
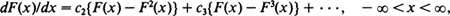where c2, c3, · ·· are arbitrary non-negative constants with 0 < c2 + c3 + · ·· <∞, and all distribution functions G and H defined by F(x)= G(c + exp(x)) and F(x) = H(c – exp(–x)), –∞ < x <∞, where c is an arbitrary real constant.
