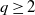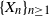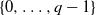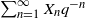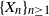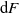A reproducing kernel approach to Lebesgue decomposition
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 13 May 2024, pp. 1-41
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Słociński–Wold decompositions for row isometries
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 14 November 2022, pp. 780-790
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Characterization of random variables with stationary digits
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 15 August 2022, pp. 931-947
- Print publication:
- December 2022
-
- Article
- Export citation
8 - Further Applications
- from Part Three - Complementary Topics
-
- Book:
- The Christoffel–Darboux Kernel for Data Analysis
- Published online:
- 31 March 2022
- Print publication:
- 07 April 2022, pp 115-124
-
- Chapter
- Export citation
Arlinskii's Iteration and its Applications
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 29 August 2018, pp. 125-133
-
- Article
- Export citation
StructuralProperties of Solutions to Total Variation Regularization Problems
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 34 / Issue 4 / July 2000
- Published online by Cambridge University Press:
- 15 April 2002, pp. 799-810
- Print publication:
- July 2000
-
- Article
- Export citation