Refine search
Actions for selected content:
16 results
5 - Linear Stability of Coherent Systems and Applications to Butler’s Conjecture
-
-
- Book:
- Moduli, Motives and Bundles
- Published online:
- 31 October 2025
- Print publication:
- 20 November 2025, pp 157-182
-
- Chapter
- Export citation
1 - Introduction to Dynamical Systems for Biology
-
- Book:
- Theoretical Biology of the Cell
- Published online:
- 05 June 2025
- Print publication:
- 19 June 2025, pp 1-40
-
- Chapter
- Export citation
6 - Two-Dimensional Laminar Boundary Layers
-
- Book:
- Flow Control
- Published online:
- 04 April 2024
- Print publication:
- 11 April 2024, pp 220-277
-
- Chapter
- Export citation
Instability of axisymmetric flow in thermocapillary liquid bridges: Kinetic and thermal energy budgets for two-phase flow with temperature-dependent material properties
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 35 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 07 July 2023, pp. 267-293
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Mean-field models for segregation dynamics
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 33 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 23 December 2020, pp. 111-132
-
- Article
- Export citation
Linear Stability Analysis of Journal Bearings Lubricated With a Non-Newtonian Rabinowitsch Fluid
-
- Journal:
- Journal of Mechanics / Volume 35 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 28 June 2017, pp. 107-112
- Print publication:
- February 2019
-
- Article
- Export citation
Linear Stability of Hyperbolic Moment Models for Boltzmann Equation
- Part of
-
- Journal:
- Numerical Mathematics: Theory, Methods and Applications / Volume 10 / Issue 2 / May 2017
- Published online by Cambridge University Press:
- 09 May 2017, pp. 255-277
- Print publication:
- May 2017
-
- Article
- Export citation
Numerical Approximations to Extremal Toric Kähler Metrics with Arbitrary Kähler Class
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 4 / November 2017
- Published online by Cambridge University Press:
- 10 January 2017, pp. 893-910
-
- Article
- Export citation
Lattice Boltzmann Modeling of Advection-Diffusion-Reaction Equations: Pattern Formation Under Uniform Differential Advection
-
- Journal:
- Communications in Computational Physics / Volume 13 / Issue 3 / March 2013
- Published online by Cambridge University Press:
- 03 June 2015, pp. 741-756
- Print publication:
- March 2013
-
- Article
- Export citation
Bifurcation Diversity in an Annular Pool Heated from Below: Prandtl and Biot Numbers Effects
-
- Journal:
- Communications in Computational Physics / Volume 13 / Issue 2 / February 2013
- Published online by Cambridge University Press:
- 03 June 2015, pp. 428-441
- Print publication:
- February 2013
-
- Article
- Export citation
Stability of Traveling Waves in Partly ParabolicSystems
-
- Journal:
- Mathematical Modelling of Natural Phenomena / Volume 8 / Issue 5 / 2013
- Published online by Cambridge University Press:
- 17 September 2013, pp. 31-47
- Print publication:
- 2013
-
- Article
- Export citation
Oblique route to turbulence
-
- Journal:
- Journal of Fluid Mechanics / Volume 674 / 10 May 2011
- Published online by Cambridge University Press:
- 28 April 2011, pp. 1-4
-
- Article
-
- You have access
- Export citation
Seuils de stabilité pour un écoulement à surface libre engendrédans une cavité cylindrique tournante à petit rapport de forme
-
- Journal:
- Mechanics & Industry / Volume 11 / Issue 5 / September 2010
- Published online by Cambridge University Press:
- 24 December 2010, pp. 339-344
- Print publication:
- September 2010
-
- Article
- Export citation
The Algebraic Multiplicity of Eigenvalues and the EvansFunction Revisited
-
- Journal:
- Mathematical Modelling of Natural Phenomena / Volume 5 / Issue 4 / 2010
- Published online by Cambridge University Press:
- 12 May 2010, pp. 269-292
- Print publication:
- 2010
-
- Article
- Export citation
Approximating the Stability Region for a Differential Equationwith a Distributed Delay
-
- Journal:
- Mathematical Modelling of Natural Phenomena / Volume 4 / Issue 2 / 2009
- Published online by Cambridge University Press:
- 26 March 2009, pp. 1-27
- Print publication:
- 2009
-
- Article
- Export citation
Green's function pointwise estimates for the modified Lax–Friedrichs scheme
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 37 / Issue 1 / January 2003
- Published online by Cambridge University Press:
- 15 March 2003, pp. 1-39
- Print publication:
- January 2003
-
- Article
- Export citation
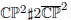 , which is conformal to an Einstein metric (the Chen–LeBrun–Weber metric). We compare our approximation to one given by Bunch and Donaldson and compute various geometric quantities. In particular, we demonstrate a small eigenvalue of the scalar Laplacian of the Einstein metric that gives numerical evidence that the Einstein metric is conformally unstable under Ricci flow.
, which is conformal to an Einstein metric (the Chen–LeBrun–Weber metric). We compare our approximation to one given by Bunch and Donaldson and compute various geometric quantities. In particular, we demonstrate a small eigenvalue of the scalar Laplacian of the Einstein metric that gives numerical evidence that the Einstein metric is conformally unstable under Ricci flow.