Complicated option pricing models attract much attention in financial industries, as they produce relatively better accurate values by taking into account more realistic assumptions such as market liquidity, uncertain volatility and so forth. We propose a new hybrid method to accurately explore the behaviour of the nonlinear pricing model in illiquid markets, which is important in financial risk management. Our method is based on the Newton iteration technique and the Fréchet derivative to linearize the model. The linearized equation is then discretized by a differential quadrature method in space and a quadratic trapezoid rule in time. It is observed through computations that the accurate solutions for the model emerge using very few grid points and time elements, compared with the finite difference method in the literature. Furthermore, this method also helps to avoid consideration of the convergence issues of the Newton approach applied to the nonlinear algebraic system containing many unknowns at each time step if an implicit method is used in time discretization. It is important to note that the Fréchet derivative supports to enhance the convergence order of the proposed iterative scheme.

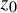
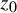
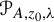Let A be a rational function of one complex variable of degree at least two, and $z_0$ its repelling fixed point with the multiplier $\unicode{x3bb} .$ A Poincaré function associated with $z_0$ is a function meromorphic on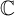 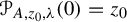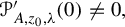${\mathbb C}$ such that , and 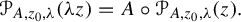In this paper, we study the following problem: given Poincaré functions 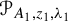and 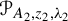, find out if there is an algebraic relation 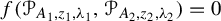between them and, if such a relation exists, describe the corresponding algebraic curve $f(x,y)=0.$ We provide a solution, which can be viewed as a refinement of the classical theorem of Ritt about commuting rational functions. We also reprove and extend previous results concerning algebraic dependencies between Böttcher functions.

We present sufficient conditions under which a given linear nonautonomous system and its nonlinear perturbation are topologically conjugated. Our conditions are of a very general form and provided that the nonlinear perturbations are well-behaved, we do not assume any asymptotic behaviour of the linear system. Moreover, the control on the nonlinear perturbations may differ along finitely many mutually complementary directions. We consider both the cases of one-sided discrete and continuous dynamics.

Rayleigh–Taylor instability occurs when a heavier fluid overlies a lighter fluid, and the two seek to exchange positions under the effect of gravity. We present a linearized theory for arbitrary three-dimensional (3D) initial disturbances that grow in time, and calculate the evolution of the interface for early times. A new spectral method is introduced for the fully 3D nonlinear problem in a Boussinesq fluid, where the interface between the light and heavy fluids is approximated with a smooth but rapid density change in the fluid. The results of large-scale numerical calculation are presented in fully 3D geometry, and compared and contrasted with the early-time linearized theory.

We consider a family of nonlinear rational recurrences of odd order which was introduced by Heideman and Hogan, and recently rediscovered in the theory of Laurent phenomenon algebras (a generalization of cluster algebras). All of these recurrences have the Laurent property, implying that for a particular choice of initial data (all initial values set to 1) they generate an integer sequence. For these particular sequences, Heideman and Hogan gave a direct proof of integrality by showing that the terms of the sequence also satisfy a linear recurrence relation with constant coefficients. Here we present an analogous result for the general solution of each of these recurrences.

In this paper, we consider two kinds of vP-fronting constructions in English and argue that they receive quite different analyses. First, we show that English vP-preposing does not have the properties that would be expected of a movement-derived dependency. Evidence for this conclusion is adduced from the licensing conditions on its occurrence, from the availability of morphological mismatches, and from reconstruction facts. By contrast, we show that English participle preposing is a well-behaved case of vP-movement, contrasting with vP-preposing with respect to reconstruction properties in particular. We propose that the differences between the two constructions follow from the interaction of two constraints: the excluded middle constraint (EMC), which rules out derivations involving spellout of linearly intermediate copies only, and the N-only constraint, which restricts movement to occurring where the trace position would license a nominal. The EMC rules out deriving vP-fronting by true movement and instead necessitates a base-generation analysis, while the N-only constraint ensures that participle preposing is only possible in limited circumstances.

In this paper we prove the conjecture of Molino that for every singular Riemannian foliation $(M,{\mathcal{F}})$, the partition $\overline{{\mathcal{F}}}$ given by the closures of the leaves of ${\mathcal{F}}$ is again a singular Riemannian foliation.

As a possible model for fluid turbulence, a Reiner–Rivlin-type equation is used to study Poiseuille–Couette flow of a viscous fluid in a rotating cylindrical pipe. The equations of motion are derived in cylindrical coordinates, and small-amplitude perturbations are considered in full generality, involving all three velocity components. A new matrix-based numerical technique is proposed for the linearized problem, from which the stability is determined using a generalized eigenvalue approach. New results are obtained in this cylindrical geometry, which confirm and generalize the predictions of previous recent studies. A possible mechanism for the transition to turbulent flow is discussed.

We present an optimal gain scheduling control design for bipedal walking with minimum tracking error. We obtained a linear approximation by linearizing the nonlinear hybrid dynamic model about a nominal periodic trajectory. This linearization allows us to identify the linear model as a linear periodic system. An optimal feedback was designed using Bellman's dynamic programming. The linear periodic system allows us to determine a linear quadratic regulator (LQR) for a single period and to set the Hamilton-Jacobi-Bellman (HJB) function in a linear quadratic form. In this way, the dynamic programming yielded an admissible continuous gain scheduling that was designed with regard to the hybrid dynamics of the system. We tuned the optimization parameters such that the tracking error and the average energy consumption are minimized. Due to linearization, we were able to examine the stability of the approximated periodic system achieved by the periodic gain according to Floquet's theory, by calculating the monodromy matrix of the closed-loop hybrid system. In addition to determining stability, the eigenvalues of this approximated monodromy matrix allowed us to evaluate the settling time of the system. This approach presents a direct method for optimal solution of locomotion control according to a given reference trajectory.

The alternating direction method of multipliers (ADMM) is applied to a constrained linear least-squares problem, where the objective function is a sum of two least-squares terms and there are box constraints. The original problem is decomposed into two easier least-squares subproblems at each iteration, and to speed up the inner iteration we linearize the relevant subproblem whenever it has no known closed-form solution. We prove the convergence of the resulting algorithm, and apply it to solve some image deblurring problems. Its efficiency is demonstrated, in comparison with Newton-type methods.

An effective linearization technique capable of equalizing IM3 products resulting from an arbitrary out-of-band blocking scenario in a wideband direct conversion receiver is presented. IM3 products are regenerated in the RF analog domain of a low-power mixed-signal feedforward path and are used to cancel analogous signal terms in the original receiver at digital baseband via adaptive equalization. The composite SAW-less receiver achieves an improvement in effective IIP3 from −7.1 to +5.3 dBm under worst-case UMTS Region 1 blocking when the feedforward path is active.

The use of digital predistortion for linearizing a millimeter-wave power amplifier (PA) is investigated. A PA operating at 38 GHz is designed using an accurate non-quasi-static transistor model, taking into account both short- and long-term memory effects. A realistic test signal is then used for the identification of a nonlinear auto-regressive moving average (NARMA) behavioral model of the PA. The NARMA-based digital predistorter is then derived and formulated in terms of basic predistortion cells, especially suitable for efficient implementation in an FPGA. The performance of the predistortion solution is preliminarily assessed by means of computer simulations.

This paper presents a linearization by static feedbacks in the robotic field, i.e. by feedback depending on the whole state space. A phenomenological approach is considered, which by using the derivation with respect to time, leads to the major results of the method. Simulation results are presented, and some aspects of the correction of the effect of the characteristic numbers are also discussed.