In the theory of dams with Markovian inputs explicit results are not usually obtained, as the theory depends very heavily on the largest eigenvalue of the matrix (pijzj) where pij are the transition probabilities of the input process. In this paper we show that explicit results can be obtained if one considers an input process of a special form. The probability distribution of the time to first emptiness is obtained for both the finite and the infinite dam, as well as the stationary distribution of the dam content for the finite dam. Explicit results are given for the case where the stationary distribution of the input process has a geometric distribution.

Some recent work on discrete time dam models has been concerned with special cases in which the input process is a Markov chain whose transition probabilities, pij, are given by 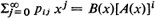where A(·) and B(·) are probability generating functions (p.g.f.'s). In this paper we obtain some results for the general situation. The convergence norm of the matrix [pijxj] is found and the results are used to obtain the p.g.f. of the first emptiness time. Distributions of the dam content are obtained and conditions are found for the existence of their limits. The p.g.f. of this distribution is so complicated that its identification in any special case is extremely difficult, or even impossible. Thus useful approximations are needed; we obtain a ‘heavy traffic’ limit theorem which suggests that under certain circumstances the limiting distribution can be approximated by an exponential distribution.