In this study we consider a freely decaying, stably stratified homogeneous magnetohydrodynamic turbulent plasma with a weak vertical background magnetic field ($\boldsymbol {B}_0=B_0\hat {\boldsymbol {z}}),$ aligned with the density gradient of strength $N$ (i.e. Brunt–Väisälä frequency). Both linear theory and direct numerical simulations (DNS) are used to analyse the flow dynamics for a Boussinesq fluid with unitary magnetic and thermal Prandtl numbers. We implemented a normal mode decomposition emphasizing different types of motions depending on whether both the Froude $F_r$ and Alfvén–Mach $M$ numbers are small or only $F_r$ is small but $M$ is finite. In the former case, there is a non-propagating (NP) mode and fast modes: Alfvén waves with frequency $\omega _a$ and magnetogravity waves with frequency $\omega _{ag}$. In the latter case, there are fast gravity waves with frequency $\omega _g$ and slow modes: NP mode and slow Alfvén waves. The numerical simulations carried out are started from initial isotropic conditions with zero initial magnetic and density fluctuations, so that the initial energy of the NP mode is strictly zero, for $0< B_0/(L_iN)\leqslant 0.12$ and a weak mean magnetic field ($B_0=0.2$ or $B_0=0.4),$ where $L_i$ denotes the isotropic integral length scale. The DNS results indicate a weak turbulence regime for which $F_r$ is small and $M$ is finite. It is found that the vertical magnetic energy as well as the energy of the NP mode are drastically reduced as $N$ increases, while there is instead a forward cascade even for the magnetic field. The contribution coming from the energy of fast (gravity) waves does not exceed $50\,\%,$ while that coming from the energy of the NP mode does not exceed $10\,\%.$ Vertical motions are more affected by the effect of stratification than by the effect of the mean magnetic field, while it is the opposite for horizontal motions. We show that the spectrum of slow (Alfvén) waves and fast (gravity) waves tends to follow the power law $k_\perp ^{-3}$ for a wide range of time, $3< t<20$. At high vertical (or horizontal) wavenumbers, the main contribution to total energy comes from the energy of slow Alfvén waves. At large and intermediate horizontal (or vertical) scales, the spectra of the energy of NP mode exhibit a flat shape.

Understanding the generation of large-scale magnetic fields and flows in magnetohydro-dynamical (MHD) turbulence remains one of the most challenging problems in astrophysical fluid dynamics. Although much work has been done on the kinematic generation of large-scale magnetic fields by turbulence, relatively little attention has been paid to the much more difficult problem in which fields and flows interact on an equal footing. The aim is to find conditions for long-wavelength instabilities of stationary MHD states. Here, we first revisit the formal exposition of the long-wavelength linear instability theory, showing how long-wavelength perturbations are governed by four mean field tensors; we then show how these tensors may be calculated explicitly under the ‘short-sudden’ approximation for the turbulence. For MHD states with relatively little disorder, the linear theory works well: average quantities can be readily calculated, and stability to long-wavelength perturbations determined. However, for disordered basic states, linear perturbations can grow without bound and the purely linear theory, as formulated, cannot be applied. We then address the question of whether there is a linear response for sufficiently weak mean fields and flows in a dynamical (nonlinear) evolution, where perturbations are guaranteed to be bounded. As a preliminary study, we first address the nature of the response in a series of one-dimensional maps. For the full MHD problem, we show that in certain circumstances, there is a clear linear response; however, in others, mean quantities – and hence the nature of the response – can be difficult to calculate.

We systematically study the dissipative anomaly in compressible magnetohydrodynamic (MHD) turbulence using direct numerical simulations, and show that the total dissipation remains finite as viscosity diminishes. The dimensionless dissipation rate $\mathcal {C}_{\varepsilon }$ fits well with the model $\mathcal {C}_{\varepsilon } = \mathcal {C}_{\varepsilon,\infty } + \mathcal {D}/R_L^-$ for all levels of flow compressibility considered here, where $R_L^-$ is the generalized large-scale Reynolds number. The asymptotic value $\mathcal {C}_{\varepsilon,\infty }$ describes the total energy transfer flux, and decreases with increase of the flow compressibility, indicating non-universality of the dimensionless dissipation rate in compressible MHD turbulence. After introducing an empirically modified dissipation rate, the data from compressible cases collapse to a form similar to the incompressible MHD case depending only on the modified Reynolds number.

Direct numerical simulations have been conducted to investigate turbulent Rayleigh– Bénard convection (RBC) of liquid metal in a cuboid vessel with aspect ratio $\varGamma =5$ under an imposed horizontal magnetic field. Flows with Prandtl number $Pr=0.033$, Rayleigh numbers ranging up to $Ra\leq 10^{7}$, and Chandrasekhar numbers up to $Q\leq 9 \times 10^6$ are considered. For weak magnetic fields, our findings reveal that a previously undiscovered decreasing region precedes the enhancement of heat transfer and kinetic energy. For moderate magnetic fields, we have reproduced the reversals of the large-scale flow, which are considered a reorganization process of the roll-like structures that were reported experimentally by Yanagisawa et al. (Phys. Rev. E, vol. 83, 2011, 036307). Nevertheless, the proposed approach of skewed-varicose instability has been substantiated as insufficient to elucidate fundamentally the phenomenon of flow reversal, an occurrence bearing a striking resemblance to the large-scale intermittency observed in magnetic channel flows. As we increase the magnetic field strength further, we observe that the energy dissipation of the system comes primarily from the viscous dissipation within the boundary layer. Consequently, the dependence of Reynolds number $Re$ on $Q$ approaches a scaling as $Re\,Pr/Ra^{2/3} \sim Q^{-1/3}$. At the same time, we find the law for the cutoff frequency that separates large quasi-two-dimensional scales from small three-dimensional ones in RBC flow, which scales with the interaction parameter as ${\sim }N^{1/3}$.

The presence of a mean magnetic field aligned with the direction of the acceleration greatly modifies the development of the Rayleigh–Taylor instability (RTI). High resolution direct numerical simulations of the Boussinesq–Navier–Stokes equations under the magnetohydrodynamics approximation reveal that, after an initial damping of the perturbations at the interface between the two miscible fluids, a rapid increase of the mixing layer is observed. Structures are significantly stretched in the vertical direction because magnetic tension prevents small-scale shear instabilities. When the vertical turbulent velocity exceeds the Alfvén velocity, the flow transitions to turbulence, structures break and an enhanced mixing occurs with strong dissipation. Afterwards, the mixing zone slows down and its growth rate is decreased compared to the hydrodynamic case. For larger magnitudes of the mean magnetic field, a strong anisotropy persists, and an increased fraction of potential energy injected into the system is lost into turbulent magnetic energy: as a consequence, the mixing zone growth rate is decreased even more. This phenomenology is embedded in a general buoyancy-drag equation, derived from simplified equations that reflect the large-scale dynamics, in which the drag coefficient is increased by the presence of turbulent magnetic energy.

The third-order law links energy transfer rates in the inertial range of magneto- hydrodynamic (MHD) turbulence with third-order structure functions. Anisotropy, a typical property in the solar wind, challenges the applicability of the third-order law with the isotropic assumption. To shed light on the energy transfer process in the presence of anisotropy, we conducted direct numerical simulations of forced MHD turbulence with normal and hyper-viscosity under various strengths of the external magnetic field ($B_0$), and calculated three forms of third-order structure function with or without averaging of the azimuthal or polar angles with respect to $B_0$ direction. Correspondingly, three estimated energy transfer rates were obtained. The result shows that the peak of normalized third-order structure function occurs at larger scales closer to the $B_0$ direction, and the maximum of longitudinal transfer rates shifts away from the $B_0$ direction at larger $B_0$. Compared with normal viscous cases, hyper-viscous cases can attain better separated inertial range, thus facilitating the estimation of the energy cascade rates. We find that the widespread use of the isotropic form of the third-order law in estimating the energy transfer rates is questionable in some cases, especially when the anisotropy arising from the mean magnetic field is inevitable. In contrast, the direction-averaged third-order structure function properly accounts for the effect of anisotropy and predicts the energy transfer rates and inertial range accurately, even at very high $B_0$. With limited statistics, the third-order structure function shows a stronger dependence on averaging of azimuthal angles than the time, especially for high $B_0$ cases. These findings provide insights into the anisotropic effect on the estimation of energy transfer rates.

Rapidly rotating convection-driven dynamos are investigated under different kinematic and magnetic boundary conditions using direct numerical simulations. At a fixed rotation rate, represented by the Ekman number 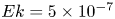$Ek=5\times 10^{-7}$, the thermal forcing is varied from $2$ to $20$ times its value at the onset of convection ($\mathcal {R}=Ra/Ra_c=2\unicode{x2013}20$, where $Ra$ is the Rayleigh number), keeping the fluid properties constant ($Pr=Pr_m=1$, where $Pr$ and $Pr_m$ are the thermal and magnetic Prandtl numbers). The statistical behaviour of the dynamos, including the force balance, energetics, and heat transport, depends on the boundary conditions that dictate both the boundary layer and the interior dynamics. At a fixed thermal forcing ($\mathcal {R}=3$), the structure and strength of the magnetic field produced by the dynamos, especially near the walls, depend on both velocity and magnetic boundary conditions. Though the leading-order force balance in the bulk remains geostrophic, the Lorentz force becomes comparable to the Coriolis force inside the thermal boundary layer with no-slip, perfectly conducting conditions. In this case, a term signifying the work done by the Lorentz force in the turbulent kinetic energy (TKE) equation is found to have some components that extract energy from the velocity field to produce the magnetic field, while some other components extract energy from the magnetic field to produce TKE. However, with no-slip, pseudo-vacuum conditions, all the components of the work done by the Lorentz force perform unidirectional energy transfer to produce magnetic energy from the kinetic energy of the fluid to sustain dynamo action. We find heat transfer enhancement in the rotating dynamo convection, as compared with non-magnetic rotating convection, with the peak enhancement lying in the range $\mathcal {R}=3\unicode{x2013}4$. For free-slip conditions, in the absence of an Ekman layer, the dynamo action may alter the heat transport significantly by suppressing the formation of large-scale vortices. However, the highest heat transfer enhancement is found at $\mathcal {R}=3$ with no-slip, perfectly conducting walls, which can be attributed to a local magnetorelaxation of the rotational constraint due to enhanced Lorentz force inside the thermal boundary layer.

Large-scale magnetic fields thread through the electrically conducting matter of the interplanetary and interstellar medium, stellar interiors and other astrophysical plasmas, producing anisotropic flows with regions of high-Reynolds-number turbulence. It is common to encounter turbulent flows structured by a magnetic field with a strength approximately equal to the root-mean-square magnetic fluctuations. In this work, direct numerical simulations of anisotropic magnetohydrodynamic (MHD) turbulence influenced by such a magnetic field are conducted for a series of cases that have identical resolution, and increasing grid sizes up to $2048^3$. The result is a series of closely comparable simulations at Reynolds numbers ranging from 1400 up to 21 000. We investigate the influence of the Reynolds number from the Lagrangian viewpoint by tracking fluid particles and calculating single-particle and two-particle statistics. The influence of Alfvénic fluctuations and the fundamental anisotropy on the MHD turbulence in these statistics is discussed. Single-particle diffusion curves exhibit mildly superdiffusive behaviours that differ in the direction aligned with the magnetic field and the direction perpendicular to it. Competing alignment processes affect the dispersion of particle pairs, in particular at the beginning of the inertial subrange of time scales. Scalings for relative dispersion, which become clearer in the inertial subrange for a larger Reynolds number, can be observed that are steeper than indicated by the Richardson prediction.

A class of exact solutions of the magnetohydrodynamic quasi-geostrophic equations (MQG), which result from rotating shallow water magnetohydrodynamics in the limit of small Rossby and magnetic Rossby numbers is constructed analytically. These solutions are magnetic modons, steady-moving dipolar vortices, which are generalizations of the well-known quasi-geostrophic modons. It is shown that various configurations of magnetic modons are possible: with or without external magnetic field, and with or without internal magnetic field trapped inside the dipole. By using the modon solutions as initial conditions for direct numerical simulations of the MQG equations, it is shown that they remain coherent for a long time, running over about a hundred deformation radii without change of form, provided the external and internal magnetic fields are not too strong, and even if a small-amplitude noise is added to initial conditions.

Astrophysical flows are often subject to both rotation and large-scale background magnetic fields. Individually, each is known to two-dimensionalize the flow in the perpendicular plane. In realistic settings, both of these effects are simultaneously present and, importantly, need not be aligned. In this work, we numerically investigate three-dimensional forced magnetohydrodynamic turbulence subject to the competing effects of global rotation and a perpendicular background magnetic field. We focus on the case of a strong background field and find that increasing the rotation rate from zero produces significant changes in the structure of the turbulent flow. Starting with a two-dimensional inverse energy cascade at zero rotation, the flow first transitions to a forward cascade of kinetic energy, then to a shear-layer dominated regime and finally to a second shear-layer regime where the kinetic energy flux is strongly suppressed and the energy transfer is mediated by the induced magnetic field. We show that the first two transitions occur at distinct values of the Rossby number, and the third occurs at a distinct value of the Lehnert number. The three-dimensional results are confirmed using an asymptotic two-dimensional, three-component model, which allows us to extend our results to the planetary-relevant case of an arbitrary angle between the rotation vector and guide field. More generally, our results demonstrate that, when considering the simultaneous limits of strong rotation and a strong guide field, the order in which those limits are taken matters in the misaligned case.

We study the influence of the shape of the plasma container on the dynamics of the reversed-field pinch (RFP). The geometries we consider are periodic cylinders with elliptical and circular-shaped cross-sections. Numerical simulations of fully nonlinear viscoresistive magnetohydrodynamics are carried out to illustrate how the plasma dynamics is affected by shaping. It is shown that independent of the plasma shape, the quantity $\beta$, comparing the hydrodynamic pressure to the magnetic pressure, decreases for increasing values of the Lundquist number, but the pressure gradient fluctuations remain roughly constant, when compared to the Lorentz force. Different elliptical shapes of the cross-section of the domain lead to the excitation of different toroidal (or axial) magnetic and dynamic modes. Furthermore, it is found that in a geometry with circular cross-section, a significant local poloidal angular momentum is observed, absent in the geometries with elliptical cross-section. Because the confinement is dominantly determined by plasma movement, and the dynamics of the velocity and magnetic field are modified by the modification of the geometry, shaping can thus affect the performance of RFP devices.

Alfvén waves as excited in black hole accretion disks and neutron star magnetospheres are the building blocks of turbulence in relativistic, magnetized plasmas. A large reservoir of magnetic energy is available in these systems, such that the plasma can be heated significantly even in the weak turbulence regime. We perform high-resolution three-dimensional simulations of counter-propagating Alfvén waves, showing that an $E_{B_{\perp }}(k_{\perp }) \propto k_{\perp }^{-2}$ energy spectrum develops as a result of the weak turbulence cascade in relativistic magnetohydrodynamics and its infinitely magnetized (force-free) limit. The plasma turbulence ubiquitously generates current sheets, which act as locations where magnetic energy dissipates. We show that current sheets form as a natural result of nonlinear interactions between counter-propagating Alfvén waves. These current sheets form owing to the compression of elongated eddies, driven by the shear induced by growing higher-order modes, and undergo a thinning process until they break-up into small-scale turbulent structures. We explore the formation of current sheets both in overlapping waves and in localized wave packet collisions. The relativistic interaction of localized Alfvén waves induces both Alfvén waves and fast waves, and efficiently mediates the conversion and dissipation of electromagnetic energy in astrophysical systems. Plasma energization through reconnection in current sheets emerging during the interaction of Alfvén waves can potentially explain X-ray emission in black hole accretion coronae and neutron star magnetospheres.

The magnetohydrodynamic (MHD) turbulence appears in engineering laboratory flows and is a common phenomenon in natural systems, e.g. stellar and planetary interiors and atmospheres and the interstellar medium. The applications in engineering are particularly interesting due to the recent advancement of tokamak devices, reaching very high plasma temperatures, thus giving hope for the production of thermonuclear fusion power. In the case of astrophysical applications, perhaps the main feature of the MHD turbulence is its ability to generate and sustain large-scale and small-scale magnetic fields. However, a crucial effect of the MHD turbulence is also the enhancement of large-scale diffusion via interactions of small-scale pulsations, i.e. the generation of the so-called turbulent viscosity and turbulent magnetic diffusivity, which typically exceed by orders of magnitude their molecular counterparts. The enhanced resistivity plays an important role in the turbulent dynamo process. Estimates of the turbulent electromotive force (EMF), including the so-called $\alpha$-effect responsible for amplification of the magnetic energy and the turbulent magnetic diffusion are desired. Here, we apply the renormalization group technique to extract the final expression for the turbulent EMF from the fully nonlinear dynamical equations (Navier–Stokes, induction equation). The simplified renormalized set of dynamical equations, including the equations for the means and fluctuations, is derived and the effective turbulent coefficients such as the viscosity, resistivity, the $\alpha$-coefficient and the Lorentz-force coefficients are explicitly calculated. The results are also used to demonstrate the influence of magnetic fields on energy and helicity spectra of strongly turbulent flows, in particular the magnetic energy spectrum.

The flow of an electrically conducting fluid in a thin disc under the action of an azimuthal Lorentz force is studied experimentally. At small forcing, the Lorentz force is balanced by either viscosity or inertia, yielding quasi-Keplerian velocity profiles. For very large current I and moderate magnetic field B, we observe a new regime, fully turbulent, which exhibits large fluctuations and a Keplerian mean rotation profile $\varOmega \sim {\sqrt {IB}}/{r^{3/2}}$, where r is the distance from the axis. In this turbulent regime, the dynamics is typical of thin layer turbulence, characterized by a direct cascade of energy towards the small scales and an inverse cascade to large scales. Finally, at very large magnetic field, this turbulent flow bifurcates to a quasi-bidimensional turbulent flow involving the formation of a large scale condensate in the horizontal plane. These results are well understood as resulting from an instability of the Bödewadt–Hartmann layers at large Reynolds number and discussed in the framework of similar astrophysical flows.

The role of the different helical components of the magnetic and velocity fields in the inverse spectral transfer of magnetic helicity is investigated through Fourier shell-to-shell transfer analysis. Magnetic helicity transfer analysis is performed on chosen data from direct numerical simulations of homogeneous isothermal compressible magnetohydrodynamic turbulence, subject to both a large-scale mechanical forcing and a small-scale helical electromotive driving. The root mean square Mach number of the hydrodynamic turbulent steady state taken as initial condition varies from 0.1 to about 11. Three physical phenomena can be distinguished in the general picture of the spectral transfer of magnetic helicity towards larger spatial scales: local inverse transfer (LIT), non-local inverse transfer (NLIT) and local direct transfer (LDT). A shell decomposition allows these three phenomena to be associated with clearly distinct velocity scales: the LDT is driven by large-scale velocity shear and associated with a direct magnetic energy cascade; the NLIT is mediated by small-scale velocity fluctuations which couple small- and large-scale magnetic structures; and the LIT by the intermediate spatial scales of the velocity field. The helical decomposition shows that like-signed helical interactions and interactions with the compressive velocity field are predominant. The latter has a high impact on the LDT and on the NLIT, but plays no role for the LIT. The locality and relative strength of the different helical contributions are mainly determined by the triad helical geometric factor, derived here in the compressible case.

We study the decay of compressible magnetohydrodynamic (MHD) turbulence, emphasizing exchanges of energy between compressive and incompressive kinetic energies, magnetic energy, and thermal energy. A recently developed high order finite difference code is employed for compressible runs with a Mach number up to 2. Varying the nature of the initial conditions (magnitudes of velocity and magnetic fluctuations), and initial Mach numbers permits examination of various dynamical regimes characterized here by the changes between different energy reservoirs. Acoustic waves are responsible for the oscillatory exchange between compressive kinetic and thermal energy through the pressure dilatation term. The results indicate that exchange between kinetic and magnetic energy is dominated by interactions involving the solenoidal velocity. Several systematic rapid adjustments are found to be reproducible with simple scalings derived from the empirical data.

High-resolution direct numerical simulations are performed to study the turbulent shear flow of liquid metal in a cylindrical container. The flow is driven by an azimuthal Lorentz force induced by the interaction between the radial electric currents injected through electrodes placed at the bottom wall and a magnetic field imposed in the axial direction. All physical parameters, are aligned with the experiment by Messadek & Moreau (J. Fluid Mech. vol. 456, 2002, pp. 137–159). The simulations recover the variations of angular momentum, velocity profiles, boundary layer thickness and turbulent spectra found experimentally to a very good precision. They further reveal a transition to small scale turbulence in the wall side layer when the Reynolds number based on Hartmann layer thickness $R$ exceeds 121, and a separation of this layer for $R \geq 145.2$. Ekman recirculations significantly influence these quantities and determine global dissipation. This phenomenology well captured by the 2-D PSM model (Pothérat, Sommeria & Moreau, J. Fluid Mech. vol. 424, 2000, pp. 75–100) until small-scale turbulence appears and incurs significant extra dissipation only captured by 3-D simulations. Secondly, we recover the theoretical law for the cutoff scale separating large quasi-two-dimensional (Q2-D) scales from small three-dimensional ones (Sommeria & Moreau, J. Fluid Mech. vol. 118, 1982, pp. 507–518), and thus establish its validity in sheared magnetohydrodynamics (MHD) turbulence. We further find that three-componentality and three-dimensionality appear concurrently and that both the frequency corresponding to the Q2-D cutoff scale and the mean energy associated with he axial component of velocity scale with the true interaction parameter $N_t$, respectively, as $0.063 N_t^{0.37}$ and $0.126N_t^{-0.92}$.

In geo- and astrophysics, low Prandtl number convective flows often interact with magnetic fields. Although a static magnetic field acts as a stabilizing force on such flow fields, we find that self-organized convective flow structures reach an optimal state where the heat transport significantly increases and convective velocities reach the theoretical free-fall limit, i.e. the maximum possible velocity a fluid parcel can achieve when its potential buoyant energy is fully converted into kinetic energy. Our measurements show that the application of a static magnetic field leads to an anisotropic, highly ordered flow structure and a decrease of the turbulent fluctuations. When the magnetic field strength is increased beyond the optimum state, Hartmann braking becomes dominant and leads to a reduction of the heat and momentum transport. The results are relevant for the understanding of magneto-hydrodynamic convective flows in planetary cores and stellar interiors in regions with strong toroidal magnetic fields oriented perpendicular to temperature gradients.