We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
In this article we will show that there are infinitely many symmetric, integral 3 × 3 matrices, with zeros on the diagonal, whose eigenvalues are all integral. We will do this by proving that the rational points on a certain non-Kummer, singular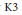 
$\text{K3}$ surface are dense. We will also compute the entire Néron–Severi group of this surface and find all low degree curves on it.
