We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
In this paper, we establish a vanishing theorem of Nadel type for the Witt multiplier ideals on threefolds over perfect fields of characteristic larger than five. As an application, if a projective normal threefold over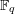 
$\mathbb{F}_{q}$ is not klt and its canonical divisor is anti-ample, then the number of the rational points on the klt-locus is divisible by 
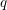$q$.
Let 
$X$ be a compact Kähler manifold and let 
$(L,{\it\varphi})$ be a pseudo-effective line bundle on 
$X$. We first define a notion of numerical dimension for pseudo-effective line bundles with singular metrics, and then discuss the properties of this numerical dimension. Finally, we prove a very general Kawamata–Viehweg–Nadel-type vanishing theorem on an arbitrary compact Kähler manifold.
