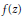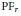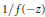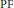Search

A well-known theorem states that if $f\left( z \right)$ generates a $\text{P}{{\text{F}}_{r}}$ sequence then $1/f\left( -z \right)$ generates a $\text{P}{{\text{F}}_{r}}$ sequence. We give two counterexamples which show that this is not true, and give a correct version of the theorem. In the infinite limit the result is sound: if $f\left( z \right)$ generates a $\text{PF}$ sequence then $1/f\left( -z \right)$ generates a $\text{PF}$ sequence.

A basic result in the theory of total positivity is that the convolution of any two Pólya frequency sequences is again a Pólya frequency sequence. The like result for binomial convolution, associated with exponential generating functions, is proved. This and similar results are used to obtain an upper bound on the probability that the union of independent random subsets of a finite set N is all of N. Parallels from the theory of reliability involving sums of random variables with increasing failure rates are noted.

Search Results

Refine search

Refine search

Actions for selected content:

2 results

Correction to a Theorem on Total Positivity

Pólya sequences, binomial convolution and the union of random sets

Search Results

Refine search

Refine search

Actions for selected content:

Save Search

2 results

Correction to a Theorem on Total Positivity

Pólya sequences, binomial convolution and the union of random sets