1 results
Alignments in two-dimensional random sets of points
-
- Journal:
- Advances in Applied Probability / Volume 12 / Issue 2 / June 1980
- Published online by Cambridge University Press:
- 01 July 2016, pp. 380-424
- Print publication:
- June 1980
-
- Article
- Export citation
-
Let n points in the plane be generated by some specified random mechanism and suppose that N(∊) of the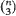
resulting triads form triangles with largest angle ≧ π – ∊. The main object of the paper is to obtain asymptotic formulae for 
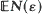and Var (N(∊)) when ∊ ↓ 0, and to solve the associated data-analytic problem of testing whether an empirical set of n points should be considered to contain too many such ∊-blunt triads in the situation where the generating mechanism is unknown and where all that can be said about the tolerance ∊ is that it must be allowed to take values anywhere in a given interval (T0, T1) (0 < T0 < T1). This problem is solved by the introduction of a plot to be called the pontogram and by the introduction of simulation-based significance tests constructed by random lateral perturbations of the data.
resulting triads form triangles with largest angle ≧ π – ∊. The main object of the paper is to obtain asymptotic formulae for 
and Var (