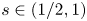We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
In this paper, we prove existence results of a one-dimensional periodic solution to equations with the fractional Laplacian of order $s\in (1/2,1)$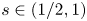
, singular nonlinearity and gradient term under various situations, including nonlocal contra-part of classical Lienard vector equations, as well other nonlocal versions of classical results know only in the context of second-order ODE. Our proofs are based on degree theory and Perron's method, so before that we need to establish a variety of priori estimates under different assumptions on the nonlinearities appearing in the equations. Besides, we obtain also multiplicity results in a regime where a priori bounds are lost and bifurcation from infinity occurs.
