We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
For a Borel set A and a homogeneous Poisson point process η in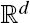 
of intensity λ>0, define the Poisson–Voronoi approximation Aη of A as a union of all Voronoi cells with nuclei from η lying in A. If A has a finite volume and perimeter, we find an exact asymptotic of E Vol(AΔ Aη) as λ→∞, where Vol is the Lebesgue measure. Estimates for all moments of Vol(Aη) and Vol(AΔ Aη) together with their asymptotics for large λ are obtained as well.
