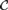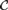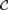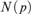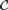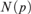A sequence of graphs is FO-convergent if the probability of satisfaction of every first-order formula converges. A graph modeling is a graph, whose domain is a standard probability space, with the property that every definable set is Borel. It was known that FO-convergent sequence of graphs do not always admit a modeling limit, but it was conjectured that FO-convergent sequences of sufficiently sparse graphs have a modeling limits. Precisely, two conjectures were proposed:

1. 1. If a FO-convergent sequence of graphs is residual, that is if for every integer d the maximum relative size of a ball of radius d in the graphs of the sequence tends to zero, then the sequence has a modeling limit.

2. 2. A monotone class of graphs ${\cal C}$ has the property that every FO-convergent sequence of graphs from ${\cal C}$ has a modeling limit if and only if ${\cal C}$ is nowhere dense, that is if and only if for each integer p there is $N\left( p \right)$ such that no graph in ${\cal C}$ contains the pth subdivision of a complete graph on $N\left( p \right)$ vertices as a subgraph.

In this article we prove both conjectures. This solves some of the main problems in the area and among others provides an analytic characterization of the nowhere dense–somewhere dense dichotomy.

The present article, which is a revised version of part of [Hu1], deals with various relations between models which might serve as exact formulations for the vague concept “similar” or “almost isomorphic”. One natural class of such formulations is equivalence in a given logic. Another way to express similarity is by potential isomorphism, i.e., isomorphism in some extension of the set-theoretic universe. The class of extensions may be restricted to give different notions of potential isomorphism. A third method is to study the winning strategies for an Ehrenfeucht-Fraïssé-game played between the two models, and the properties of the resulting equivalence and nonequivalence trees.

The basic question studied here is whether one such notion of similarity implies another. Some implications and counterexamples listed in this part are previously known or trivial, but all are mentioned for completeness' sake. Only models of cardinality ℵ1 are considered. Some results are therefore connected with the Continuum Hypothesis.