For each poset H whose Hasse diagram is a tree of height k, we show that the largest size of a family of subsets of [n]={1,. . ., n} not containing H as an induced subposet is asymptotic to . This extends a result of Bukh [1], which in turn generalizes several known results including Sperner's theorem.

A causal set is a countably infinite poset in which every element is above finitely many others; causal sets are exactly the posets that have a linear extension with the order-type of the natural numbers; we call such a linear extension a natural extension. We study probability measures on the set of natural extensions of a causal set, especially those measures having the property of order-invariance: if we condition on the set of the bottom k elements of the natural extension, each feasible ordering among these k elements is equally likely. We give sufficient conditions for the existence and uniqueness of an order-invariant measure on the set of natural extensions of a causal set.

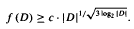A subset F of an ordered set X is a fibre of X if F intersects every maximal antichain of X. We find a lower bound on the function ƒ (D), the minimum fibre size in the distributive lattice D, in terms of the size of D. In particular, we prove that there is a constant c such that In the process we show that minimum fibre size is a monotone property for a certain class of distributive lattices. This fact depends upon being able to split every maximal antichain of this class of distributive lattices into two parts so that the lattice is the union of the upset of one part and the downset of the other.