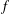 $f$-MAXIMAL SPACELIKE HYPERSURFACES IN CERTAIN WEIGHTED MANIFOLDS
$f$-MAXIMAL SPACELIKE HYPERSURFACES IN CERTAIN WEIGHTED MANIFOLDS
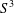 $S^{3}$ WITH CONSTANT SECTIONAL CURVATURE IN
$S^{3}$ WITH CONSTANT SECTIONAL CURVATURE IN 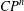 $\mathit{CP}^{n}$
$\mathit{CP}^{n}$
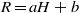 $R= aH+ b$
$R= aH+ b$