Article contents
ON THE EXISTENCE OF 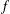 $f$-MAXIMAL SPACELIKE HYPERSURFACES IN CERTAIN WEIGHTED MANIFOLDS
$f$-MAXIMAL SPACELIKE HYPERSURFACES IN CERTAIN WEIGHTED MANIFOLDS
Published online by Cambridge University Press: 02 May 2017
Abstract
We apply a mean-value inequality for positive subsolutions of the 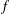 $f$-heat operator, obtained from a Sobolev embedding, to prove a nonexistence result concerning complete noncompact
$f$-heat operator, obtained from a Sobolev embedding, to prove a nonexistence result concerning complete noncompact 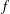 $f$-maximal spacelike hypersurfaces in a class of weighted Lorentzian manifolds. Furthermore, we establish a new Calabi–Bernstein result for complete noncompact maximal spacelike hypersurfaces in a Lorentzian product space.
$f$-maximal spacelike hypersurfaces in a class of weighted Lorentzian manifolds. Furthermore, we establish a new Calabi–Bernstein result for complete noncompact maximal spacelike hypersurfaces in a Lorentzian product space.
Keywords
- Type
- Research Article
- Information
- Bulletin of the Australian Mathematical Society , Volume 96 , Issue 2 , October 2017 , pp. 317 - 325
- Copyright
- © 2017 Australian Mathematical Publishing Association Inc.
Footnotes
The second author is partially supported by CNPq, Brazil, grant 303977/2015-9.
References
- 1
- Cited by


