1 results
On Semi-Primary Self-Injective Rings and Faith's Quasi-Frobenius Conjecture
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 58 / Issue 1 / February 2015
- Published online by Cambridge University Press:
- 10 December 2014, pp. 219-229
-
- Article
- Export citation
-
A long-standing conjecture of Faith in ring theory states that a left self-injective semi-primary ring A is necessarily a quasi-Frobenius ring. We propose a new method for approaching this conjecture, and prove it under some mild conditions; we show that if the simple A-modules are at most countably generated over a subring of the centre of A, then the conjecture holds. Also, the conjecture holds for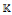
algebras A over sufficiently large fields, i.e. if the cardinality of 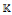is larger than the dimension of the simple A-modules (or of A/Jac(A)). This effectively proves the conjecture in many situations, and we obtain several previously known results on this problem as a consequence.
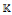algebras 