1 results
Limit distributions of the number of renewals and waiting times
-
- Journal:
- Journal of Applied Probability / Volume 13 / Issue 2 / June 1976
- Published online by Cambridge University Press:
- 14 July 2016, pp. 301-312
- Print publication:
- June 1976
-
- Article
- Export citation
-
Let {Xn} be an infinite sequence of independent non-negative random variables. Let the distribution function of Xi, i = 1, 2, …, be either F1 or F2 where F1 and F2 are distinct. Set Sn = X1 + X2 + … + Xn and for t > 0 define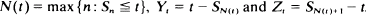
and Zt = SN(t)+1 – t. The limit distributions of N(t), Yt and Zt as t → ∞ are obtained when F1 and F2 are in the domains of attraction of stable laws with exponents α1 and α2, respectively and Sn properly normalised has the composition of these two stable laws as its limit distribution.
and 