1 results
Stability of maxima of random variables defined on a Markov chain
-
- Journal:
- Advances in Applied Probability / Volume 4 / Issue 2 / August 1972
- Published online by Cambridge University Press:
- 01 July 2016, pp. 285-295
- Print publication:
- August 1972
-
- Article
- Export citation
-
Consider maxima Mn of a sequence of random variables defined on a finite Markov chain. Necessary and sufficient conditions for the existence of normalizing constants Bn such that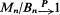
are given. The problem can be reduced to studying maxima of i.i.d. random variables drawn from a finite product of distributions πi=1mHi(x). The effect of each factor Hi(x) on the behavior of maxima from πi=1mHi is analyzed. Under a mild regularity condition, Bn can be chosen to be the maximum of the m quantiles of order (1 - n-1) of the H's.
are given. The problem can be reduced to studying maxima of i.i.d. random variables drawn from a finite product of distributions π