1 results
STRICT TOPOLOGY AS A MIXED TOPOLOGY ON LEBESGUE SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 84 / Issue 3 / December 2011
- Published online by Cambridge University Press:
- 06 September 2011, pp. 504-515
- Print publication:
- December 2011
-
- Article
-
- You have access
- Export citation
-
Let X be a locally compact space, and 𝔏∞0(X,ι) be the space of all essentially bounded ι-measurable functions f on X vanishing at infinity. We introduce and study a locally convex topology β1(X,ι) on the Lebesgue space 𝔏1(X,ι) such that the strong dual of (𝔏1(X,ι),β1(X,ι)) can be identified with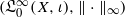
. Next, by showing that β1(X,ι) can be considered as a natural mixed topology, we deduce some of its basic properties. Finally, as an application, we prove that L1 (G) , the group algebra of a locally compact Hausdorff topological group G, equipped with the convolution multiplication is a complete semitopological algebra under the β1 (G) topology.
. Next, by showing that 