1 results
Inheritance of strong mixing and weak dependence under renewal sampling
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 14 October 2022, pp. 435-451
- Print publication:
- June 2023
-
- Article
-
- You have access
- HTML
- Export citation
-
Let X be a continuous-time strongly mixing or weakly dependent process and let T be a renewal process independent of X. We show general conditions under which the sampled process
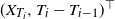$(X_{T_i},T_i-T_{i-1})^{\top}$
is strongly mixing or weakly dependent. Moreover, we explicitly compute the strong mixing or weak dependence coefficients of the renewal sampled process and show that exponential or power decay of the coefficients of X is preserved (at least asymptotically). Our results imply that essentially all central limit theorems available in the literature for strongly mixing or weakly dependent processes can be applied when renewal sampled observations of the process X are at our disposal.
