We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Following ideas used by Drewnowski and Wilansky we prove that if 
$I$ is an infinite dimensional and infinite codimensional closed ideal in a complete metrizable locally solid Riesz space and $I$ does not contain any order copy of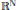 
${{\mathbb{R}}^{\mathbb{N}}}$ then there exists a closed, separable, discrete Riesz subspace 
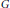$G$ such that the topology induced on 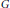$G$ is Lebesgue, 
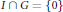$I\,\bigcap \,G\,=\,\left\{ 0 \right\}$, and 
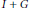$I\,+\,G$ is not closed.
