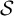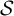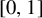1 results
On partial rigidity of
$\mathcal {S}$-adic subshifts
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 24 February 2025, pp. 1-41
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
-
We develop combinatorial tools to study partial rigidity within the class of minimal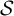
$\mathcal {S}$-adic subshifts. By leveraging the combinatorial data of well-chosen Kakutani–Rokhlin partitions, we establish a necessary and sufficient condition for partial rigidity. Additionally, we provide an explicit expression to compute the partial rigidity rate and an associated partial rigidity sequence. As applications, we compute the partial rigidity rate for a variety of constant length substitution subshifts, such as the Thue–Morse subshift, where we determine a partial rigidity rate of 2/3. We also exhibit non-rigid substitution subshifts with partial rigidity rates arbitrarily close to 1 and, as a consequence, using products of the aforementioned substitutions, we obtain that any number in 
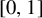$[0, 1]$ is the partial rigidity rate of a system.
