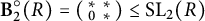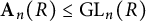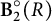2 results
On the Finiteness length of some soluble linear groups
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 5 / October 2022
- Published online by Cambridge University Press:
- 21 April 2021, pp. 1209-1243
- Print publication:
- October 2022
-
- Article
- Export citation
Homology stability for unitary groups over S-arithmetic rings
-
- Journal:
- Journal of K-Theory / Volume 8 / Issue 2 / October 2011
- Published online by Cambridge University Press:
- 05 November 2010, pp. 293-322
- Print publication:
- October 2011
-
- Article
- Export citation