1 results
Seneta constants for the supercritical Bellman–Harris process
-
- Journal:
- Advances in Applied Probability / Volume 14 / Issue 4 / December 1982
- Published online by Cambridge University Press:
- 01 July 2016, pp. 732-751
- Print publication:
- December 1982
-
- Article
- Export citation
-
Let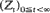
be a supercritical Bellman-Harris process with finite offspring mean. Cohn [17] has shown that there always exist constants Ct such that limt→∞Zt/Ct = W almost surely for some non-degenerate random variable W. In this paper we give an alternative proof, based on the study of (Zt) as a point process. Our methods are to some extent analytical and parallel Seneta's [18] and Heyde's [11] approaches in the case of the Galton–Watson process. We further identify Ct as 1/(–log Ft(–1)(γ)), where Ft(γ) = E(γzt), i.e. the norming constants found by Seneta [18] for the Galton–Watson process, apply also to the Bellman-Harris process. Finally we derive a weak law of large numbers for W, prove that W is continuous on (0,∞) and show that W has [0,∞) as its support.
be a supercritical Bellman-Harris process with finite offspring mean. Cohn [17] has shown that there always exist constants 