A number of stochastic queueing systems exhibit an interesting phenomenon known as the cut-off phenomenon. A properly scaled version of the distance between the transient process and the stationary one converges to a step function as the initial load converges to infinity. The purpose of this paper is to promote the idea that this phenomenon is a direct consequence of the coupling between the two processes, being thus generalizable to systems lacking any kind of Markovian structure.

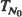We analyze a stable GI/G/1 queue that starts operating at time t = 0 with N0 ≠ 0 customers. First, we analyze the time required for this queue to empty for the first time. Under the assumption that both the interarrival and the service time distributions are of the exponential type, we prove that 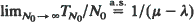, where λ and μ are the arrival and the service rates. Furthermore, assuming in addition that the interarrival time distribution is of the non-lattice type, we show that the settling time of the queue is essentially equal to N0/(μ –λ); that is, we prove that where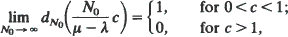 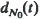is the total variation distance between the distribution of the number of customers in the system at time t and its steady-state distribution. Finally, we show that there is a similarity between the queue we analyze and a simple fluid model.