A sequence of random triangles is constructed by choosing successively the three vertices of one triangle at random in the interior of its predecessor. A way is found to prove that the shapes of these triangles converge, almost surely, to collinear shapes, thus closing a gap in one of the central arguments of Mannion [5]. The new approach is based on a representation of the triangle process by a sequence of products of i.i.d. random matrices. We succeed in calculating the corresponding Lyapounov exponent.

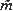This paper is concerned with the shape-density for a random triangle whose vertices are randomly labelled and i.i.d.-uniform in a compact convex polygon 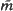K. In earlier work we have already shown that there is a network of curves (the singular tessellation T(K)) across which suffers discontinuities of form. 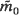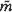In two papers which will appear in parallel with this, Hui-lin Le finds explicit formulae for (i) the form of within the basic tile 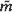T0 of T(K), and (ii) the jump-functions which link the local forms of on either side of any curve separating two tiles. Here we exploit these calculations to find 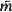in the most general case. We describe the geometry of 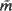T(K), we examine the real-analytic structure of within a tile, and we establish by analytic continuation an explicit formula giving 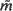in an arbitrary tile 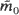T as the sum of the basic-tile function and the members of a finite sequence of jump-functions along a ‘stepping-stone' tile-to-tile route from T0 to T. Finally we comment on some of the problems that arise in the use of this formula in studies relating to the applications in archaeology and astronomy.

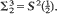The paper starts with a simple direct proof that . A new formula is given for the shape-density for a triangle whose vertices are i.i.d.-uniform in a compact convex set 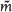K, and an exact evaluation of that shape-density is obtained when K is a circular disk. An (x, y)-diagram for an auxiliary shape-density is then introduced. When 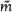K = circular disk, it is shown that is virtually constant over a substantial region adjacent to the relevant section of the collinearity locus, large enough to contain the work-space for most collinearity studies, and particularly appropriate when the ‘strip’ method is used to assess near-collinearity.