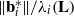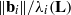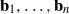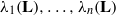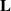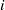Gama and Nguyen [‘Finding short lattice vectors within Mordell’s inequality’, in: Proceedings of the 40th Annual ACM Symposium on Theory of Computing, New York, 2008, 257–278] have presented slide reduction which is currently the best SVP approximation algorithm in theory. In this paper, we prove the upper and lower bounds for the ratios 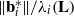 \Vert { \mathbf{b} }_{i}^{\ast } \Vert / {\lambda }_{i} (\mathbf{L} ) and
\Vert { \mathbf{b} }_{i}^{\ast } \Vert / {\lambda }_{i} (\mathbf{L} ) and 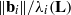 \Vert {\mathbf{b} }_{i} \Vert / {\lambda }_{i} (\mathbf{L} ), where
\Vert {\mathbf{b} }_{i} \Vert / {\lambda }_{i} (\mathbf{L} ), where 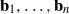 {\mathbf{b} }_{1} , \ldots , {\mathbf{b} }_{n} is a slide reduced basis and
{\mathbf{b} }_{1} , \ldots , {\mathbf{b} }_{n} is a slide reduced basis and 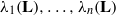 {\lambda }_{1} (\mathbf{L} ), \ldots , {\lambda }_{n} (\mathbf{L} ) denote the successive minima of the lattice
{\lambda }_{1} (\mathbf{L} ), \ldots , {\lambda }_{n} (\mathbf{L} ) denote the successive minima of the lattice 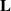 \mathbf{L} . We define generalised slide reduction and use slide reduction to approximate
\mathbf{L} . We define generalised slide reduction and use slide reduction to approximate 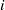 i-SIVP, SMP and CVP. We also present a critical slide reduced basis for blocksize 2.
i-SIVP, SMP and CVP. We also present a critical slide reduced basis for blocksize 2.