1 results
On the determination of a distribution by its median residual life function: a functional equation
-
- Journal:
- Journal of Applied Probability / Volume 21 / Issue 1 / March 1984
- Published online by Cambridge University Press:
- 14 July 2016, pp. 120-128
- Print publication:
- March 1984
-
- Article
- Export citation
-
In reliability studies, it is well known that the mean residual life function determines the distribution function uniquely. In this paper we show how closely we can determine a distribution when its median residual life function M[S | t] is known. This amounts to solving the functional equation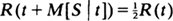
, where R is the reliability function. We actually study a more general functional equation f(φ(t)) = sf(t) called Schroder's equation. It is shown that, under mild assumptions on φ, the solution is of the form f(t) = f0(t)k(log f0 (t)), where f0 is a well-behaved particular solution which can be constructed and k is a periodic function; thus the solution is not unique. Two examples are solved to illustrate the method. Finally, these examples are used to solve the problem of linear M[S | t] studied by Schmittlein and Morrison. As an extra benefit, all of our results hold equally well for the more general sth percentile residual life function.
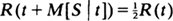, where 