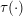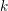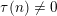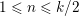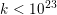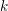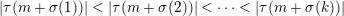3 results
Random ordering in modulus of consecutive Hecke eigenvalues of primitive forms
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 11 / November 2018
- Published online by Cambridge University Press:
- 18 October 2018, pp. 2441-2461
- Print publication:
- November 2018
-
- Article
- Export citation
A Remark on a Modular Analogue of the Sato–Tate Conjecture
-
- Journal:
- Canadian Mathematical Bulletin / Volume 50 / Issue 2 / 01 June 2007
- Published online by Cambridge University Press:
- 20 November 2018, pp. 234-242
- Print publication:
- 01 June 2007
-
- Article
-
- You have access
- Export citation
A Sato–Tate Law for Drinfeld Modules
-
- Journal:
- Compositio Mathematica / Volume 138 / Issue 2 / September 2003
- Published online by Cambridge University Press:
- 04 December 2007, pp. 189-197
- Print publication:
- September 2003
-
- Article
-
- You have access
- Export citation