1 results
Involution pipe dreams
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 5 / October 2022
- Published online by Cambridge University Press:
- 14 May 2021, pp. 1310-1346
- Print publication:
- October 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
-
Involution Schubert polynomials represent cohomology classes of K-orbit closures in the complete flag variety, where K is the orthogonal or symplectic group. We show they also represent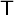
$\mathsf {T}$
-equivariant cohomology classes of subvarieties defined by upper-left rank conditions in the spaces of symmetric or skew-symmetric matrices. This geometry implies that these polynomials are positive combinations of monomials in the variables 
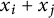$x_i + x_j$
, and we give explicit formulas of this kind as sums over new objects called involution pipe dreams. Our formulas are analogues of the Billey–Jockusch–Stanley formula for Schubert polynomials. In Knutson and Miller’s approach to matrix Schubert varieties, pipe dream formulas reflect Gröbner degenerations of the ideals of those varieties, and we conjecturally identify analogous degenerations in our setting.
