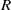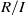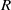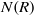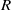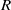2 results
USING IDEALS TO PROVIDE A UNIFIED APPROACH TO UNIQUELY CLEAN RINGS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 96 / Issue 2 / April 2014
- Published online by Cambridge University Press:
- 01 April 2014, pp. 258-274
- Print publication:
- April 2014
-
- Article
-
- You have access
- Export citation
ORE EXTENSIONS OF WEAK ZIP RINGS*
-
- Journal:
- Glasgow Mathematical Journal / Volume 51 / Issue 3 / September 2009
- Published online by Cambridge University Press:
- 01 September 2009, pp. 525-537
- Print publication:
- September 2009
-
- Article
-
- You have access
- Export citation