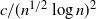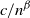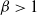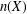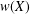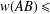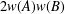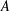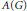19 results
5 - Growth, Dimension, and Heat Kernel
- from Part II - Results and Applications
-
- Book:
- Harmonic Functions and Random Walks on Groups
- Published online:
- 16 May 2024
- Print publication:
- 23 May 2024, pp 161-195
-
- Chapter
- Export citation
6 - Norms and Procrustes Problems
-
- Book:
- Linear Algebra for Data Science, Machine Learning, and Signal Processing
- Published online:
- 01 November 2024
- Print publication:
- 16 May 2024, pp 197-237
-
- Chapter
- Export citation
19 - Norms and Matrix Norms
-
- Book:
- Matrix Mathematics
- Published online:
- 29 September 2023
- Print publication:
- 25 May 2023, pp 390-405
-
- Chapter
- Export citation
20 - Positive and Nonnegative Matrices
-
- Book:
- Matrix Mathematics
- Published online:
- 29 September 2023
- Print publication:
- 25 May 2023, pp 406-416
-
- Chapter
- Export citation
Co-spectral radius of intersections
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 2 / February 2024
- Published online by Cambridge University Press:
- 17 April 2023, pp. 509-523
- Print publication:
- February 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE SIZE, SPECTRAL RADIUS, DISTANCE SPECTRAL RADIUS AND FRACTIONAL MATCHINGS IN GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 2 / October 2023
- Published online by Cambridge University Press:
- 13 January 2023, pp. 187-199
- Print publication:
- October 2023
-
- Article
- Export citation
4 - Norms and Matrix Conditioning
- from Part I - Numerical Linear Algebra
-
- Book:
- Classical Numerical Analysis
- Published online:
- 29 September 2022
- Print publication:
- 20 October 2022, pp 73-87
-
- Chapter
- Export citation
Two-type linear-fractional branching processes in varying environments with asymptotically constant mean matrices
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 07 February 2022, pp. 224-255
- Print publication:
- March 2022
-
- Article
- Export citation
15 - Tropical Markov Dynamics and Cayley Cubic
-
-
- Book:
- Integrable Systems and Algebraic Geometry
- Published online:
- 19 March 2020
- Print publication:
- 02 April 2020, pp 383-394
-
- Chapter
- Export citation
IMPROVED INEQUALITIES FOR THE NUMERICAL RADIUS: WHEN INVERSE COMMUTES WITH THE NORM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 2 / April 2018
- Published online by Cambridge University Press:
- 02 February 2018, pp. 293-296
- Print publication:
- April 2018
-
- Article
-
- You have access
- Export citation
CONTINUITY OF THE HAUSDORFF DIMENSION FOR GRAPH-DIRECTED SYSTEMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 3 / December 2016
- Published online by Cambridge University Press:
- 16 August 2016, pp. 471-478
- Print publication:
- December 2016
-
- Article
-
- You have access
- Export citation
Numerical Solution to the Multi-Term Time Fractional Diffusion Equation in a Finite Domain
- Part of
-
- Journal:
- Numerical Mathematics: Theory, Methods and Applications / Volume 9 / Issue 3 / August 2016
- Published online by Cambridge University Press:
- 20 July 2016, pp. 337-357
- Print publication:
- August 2016
-
- Article
-
- You have access
- Export citation
Maximizing the Index of Trees with Given Domination Number
-
- Journal:
- Canadian Mathematical Bulletin / Volume 57 / Issue 3 / 01 September 2014
- Published online by Cambridge University Press:
- 20 November 2018, pp. 520-525
- Print publication:
- 01 September 2014
-
- Article
-
- You have access
- Export citation
Pseudo-Tournament Matrices and Their Eigenvalues
-
- Journal:
- East Asian Journal on Applied Mathematics / Volume 4 / Issue 3 / August 2014
- Published online by Cambridge University Press:
- 28 May 2015, pp. 205-221
- Print publication:
- August 2014
-
- Article
- Export citation
Asymptotic Stability of an Eikonal Transformation Based ADI Method for the Paraxial Helmholtz Equation at High Wave Numbers
-
- Journal:
- Communications in Computational Physics / Volume 12 / Issue 4 / October 2012
- Published online by Cambridge University Press:
- 20 August 2015, pp. 1275-1292
- Print publication:
- October 2012
-
- Article
- Export citation
Existence results for nonlinear periodic boundary-value problems
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 52 / Issue 1 / February 2009
- Published online by Cambridge University Press:
- 02 February 2009, pp. 79-95
-
- Article
-
- You have access
- Export citation
Particle approximations of Lyapunov exponents connected to Schrödinger operators and Feynman–Kac semigroups
-
- Journal:
- ESAIM: Probability and Statistics / Volume 7 / March 2003
- Published online by Cambridge University Press:
- 15 May 2003, pp. 171-208
- Print publication:
- March 2003
-
- Article
- Export citation
An asymptotic formula for the Bayes risk in discriminating between two Markov chains
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 38 / Issue A / 2001
- Published online by Cambridge University Press:
- 14 July 2016, pp. 131-141
- Print publication:
- 2001
-
- Article
- Export citation
The Spectral Radius of a Non-Negative Matrix
-
- Journal:
- Canadian Mathematical Bulletin / Volume 21 / Issue 1 / 01 March 1978
- Published online by Cambridge University Press:
- 20 November 2018, pp. 113-114
- Print publication:
- 01 March 1978
-
- Article
-
- You have access
- Export citation