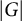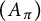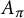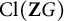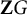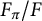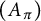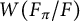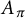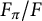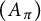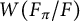Refine search
Actions for selected content:
1 results
On the square root of the inverse different
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 11 January 2023, pp. 283-318
- Print publication:
- February 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation