Definable stationary sets, and specifically, ordinal definable ones, play a significant role in the study of canonical inner models of set theory and the class HOD of hereditarily ordinal definable sets. Fixing a certain notion of definability and an uncountable cardinal, one can consider the associated family of definable closed unbounded sets. In this paper, we study the extent to which such families can approximate the full closed unbounded filter and their dependence on the defining complexity. Focusing on closed unbounded subsets of a cardinal $\kappa $ which are $\Sigma _1$-definable in parameters from H${}_\kappa $ and ordinal parameters, we show that the ability of such closed unbounded sets to well approximate the closed unbounded filter on $\kappa $ can highly vary and strongly depends on key properties of the underlying universe of set theory.

We study the consequences of stationary and semi-stationary set reflection. We show that the semi-stationary reflection principle implies the Singular Cardinal Hypothesis, the failure of the weak square principle, etc. We also consider two cardinal tree properties introduced recently by Weiss, and prove that they follow from stationary and semi-stationary set reflection augmented with a weak form of Martin’s Axiom. We also show that there are some differences between the two reflection principles, which suggests that stationary set reflection is analogous to supercompactness, whereas semi-stationary set reflection is analogous to strong compactness.

If S, T are stationary subsets of a regular uncountable cardinal κ, we say that S reflects fully in T, S < T, if for almost all α ∈ T (except a nonstationary set) S ∩ α stationary in α. This relation is known to be a well-founded partial ordering. We say that a given poset P is realized by the reflection ordering if there is a maximal antichain 〈Xp: p ∈ P〉 of stationary subsets of Reg(κ) so that

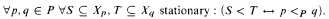
We prove that if 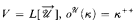, and P is an arbitrary well-founded poset of cardinality ≤ κ+ then there is a generic extension where P is realized by the reflection ordering on κ.

A stationary subset S of a regular uncountable cardinal κreflects fully at regular cardinals if for every stationary set T ⊆ κ of higher order consisting of regular cardinals there exists an α Є T such that S ∩ α is a stationary subset of α. Full Reflection states that every stationary set reflects fully at regular cardinals. We will prove that under a slightly weaker assumption than κ having the Mitchell order κ++ it is consistent that Full Reflection holds at every λ ≤ κ and κ is measurable.