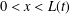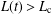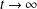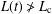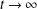2 results
CRITICAL LENGTH FOR THE SPREADING–VANISHING DICHOTOMY IN HIGHER DIMENSIONS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 62 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 19 June 2020, pp. 3-17
-
- Article
-
- You have access
- Export citation
Stability of flat interfaces during semidiscrete solidification
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 36 / Issue 4 / July 2002
- Published online by Cambridge University Press:
- 15 September 2002, pp. 573-595
- Print publication:
- July 2002
-
- Article
- Export citation