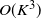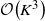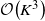In a rare life-threatening disease setting the number of patients in the trial is a high proportion of all patients with the condition (if not all of them). Further, this number is usually not enough to guarantee the required statistical power to detect a treatment effect of a meaningful size. In such a context, the idea of prioritizing patient benefit over hypothesis testing as the goal of the trial can lead to a trial design that produces useful information to guide treatment, even if it does not do so with the standard levels of statistical confidence. The idealized model to consider such an optimal design of a clinical trial is known as a classic multi-armed bandit problem with a finite patient horizon and a patient benefit objective function. Such a design maximizes patient benefit by balancing the learning and earning goals as data accumulates and given the patient horizon. On the other hand, optimally solving such a model has a very high computational cost (many times prohibitive) and more importantly, a cumbersome implementation, even for populations as small as a hundred patients. Several computationally feasible heuristic rules to address this problem have been proposed over the last 40 years in the literature. In this paper, we study a novel heuristic approach to solve it based on the reformulation of the problem as a Restless bandit problem and the derivation of its corresponding Whittle Index (WI) rule. Such rule was recently proposed in the context of a clinical trial in Villar, Bowden, and Wason [16]. We perform extensive computational studies to compare through both exact value calculations and simulated values the performance of this rule, other index rules and simpler heuristics previously proposed in the literature. Our results suggest that for the two and three-armed case and a patient horizon less or equal than a hundred patients, all index rules are a priori practically identical in terms of the expected proportion of success attained when all arms start with a uniform prior. However, we find that a posteriori, for specific values of the parameters of interest, the index policies outperform the simpler rules in every instance and specially so in the case of many arms and a larger, though still relatively small, total number of patients with the diseases. The very good performance of bandit rules in terms of patient benefit (i.e., expected number of successes and mean number of patients allocated to the best arm, if it exists) makes them very appealing in context of the challenge posed by drug development and treatment for rare life-threatening diseases.
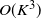 $O(K^3)$ algorithm to compute whittle index – CORRIGENDUM
$O(K^3)$ algorithm to compute whittle index – CORRIGENDUM
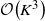 $\mathcal{O}\!\left(K^3\right)$ algorithm to compute Whittle index
$\mathcal{O}\!\left(K^3\right)$ algorithm to compute Whittle index