1 results
Distortion mismatch in the quantization of probability measures
-
- Journal:
- ESAIM: Probability and Statistics / Volume 12 / 2008
- Published online by Cambridge University Press:
- 23 January 2008, pp. 127-153
- Print publication:
- 2008
-
- Article
- Export citation
-
We elucidate the asymptotics of the Ls -quantization error induced by a sequence of Lr -optimal n-quantizers of aprobability distribution P on $\mathbb{R}^d$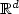
when s > r. In particular we show that under natural assumptions, the optimal rate is preserved aslong as s < r+d (and for everys in the case of a compactly supported distribution). We derive some applications of these results to the error bounds for quantization based cubatureformulae in numerical integration on $\mathbb{R}^d$ 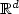and on the Wiener space.
